The Beautiful Modernism Of Oliver Byrne’s, The First Six Books Of The Elements Of Euclid, 1847


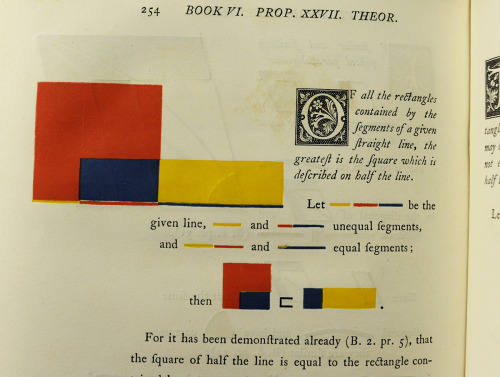



The beautiful modernism of Oliver Byrne’s, The First Six Books of the Elements of Euclid, 1847
More Posts from Bsdndprplplld and Others
Artificial intelligence makes accurate sheep counting.
7 X 2022
my first week is over. I'm tired and I can tell already that it will be a hard semester. I have already spent more than 15 hours on my complex analysis homework and I solved 1 problem out of 10, ugh
this subject is gonna give me major impostor syndrom lmao I know that these problems are putnam level difficulty but it's frustrating to have spent the whole day on something and fail. and I'm not kidding, I have a book on problem solving techinques for putnam and the exercises there are easier than those we do in class
one could say I'm bragging but it doesn't mean anything if I can complete only 1 of 10 problems which is a trivial corollary from Vieta's and took me about 4 hours to realize anyway
algebra homework was relatively easy, I discussed it with a few people who also take the course and together we completed the whole thing
for now I still have the motivation to try to look good so this week I've been pulling off dark academia aesthetic


I am afraid of my brain because it likes to give me meltdowns right when I need my cognitive performance to be reliable. I spent the whole holiday working on coping skills so I could spend less time sitting on the floor and crying
I spend most of the time with my boyfriend studying together. having a body double really helps

My favorite example of girl math is when David Hilbert and Albert Einstein couldn't solve how energy conservation worked in general relativity, so Hilbert asked Emmy Noether about it and she solved it for them.
12 XII 2022
I have a test at the end of this week so I am mostly grinding for that, kinda ignoring other things along the way, planning to catch up with them during the christmas break
the new update for my tablet's OS brought the option to insert pictures into the notes, so now I can paste the problem statements directly from the book. I am not sure if this is actually efficient but it surely looks better and the notes are more readable


(I can't vouch for the correctness of those tho lol I just started learning about the Rouché's theorem)
I have been trying to keep up with the material discussed in lectures on commutative algebra and agebraic methods. with each lecture there is a set of homework problems to solve and I predefined a standard for myself that this week it's alright if I don't do the homework because grinding for the test is more important

I made some pretty notes on valuation rings
during the break I need to study finite and integral ring maps and valuation rings for commutative algebra course; resolutions, derived functors and universal coefficients theorem for algebraic methods course. I feel pretty good about the test that's coming up. sure, you can never be too prepared but so far I've been able to solve a good part of the problems I tried, so I should be ok
i gotta say i don't buy all them planning strategies and tips that require more effort than just sitting and doing the work
i mean that might help some people but i find that when i am doing something important to me i need no plans nor do i need motivation, i also don't procrastinate, everything falls into its right place
and if achieving something takes so much effort in preparation, is this even supposed to be a thing? idk, maybe that's the reason why i have no external proof of my work lol
7 XI 2022
I think I found an advisor and a topic for the bsc thesis! or rather they found me
one of the teachers that prepares us for writing our theses approached me and started asking about homology I mentioned during our presentation, he wanted to know what courses I took and how familiar I am with that stuff. I told him that I know a bit about homology only from self-study but I enjoyed everything from algebraic topo so far and I would be happy to write about something from that. "ok then I'll find the right topic for you" was his response. then he suggested I read Groups of Homotopy Spheres by Milnor and Kervaire and write about surgery theory. I was sold the moment I heard that name, it's almost as funny as writing about the hairy ball




so there she is, very high level, very complicated. I barely skimmed the first half of that 34-page paper, it's gonna take a lot of work before I learn the basics necessary to even comprehend what is going on. it feels good to be noticed tho, I'm so happy to start writing asap
other than that my mood hasn't been in a great place, because commutative algebra is super hard and I am struggling to find the right resources to study. the last thing we did was tensor product and I've been procrastinating actually studying it by making pretty notes lol

I found a textbook that seems decent. the theory is very thoroughly explained here and there are plenty of exercises ranging from easy to difficult ones

recently I've been trying a new method of tracking, which is instead of writing to-do lists, I write down what I did each day, here is what it looks like for now:

I find it much less anxiety-inducing than the to-do approach because I know damn well what I need to do and writing down what I actually completed feels much better than crossing things off of the list
this week I hope to study the tensor product, representable functors (yoneda is still not done with me) and probably start the complex analysis homework. if I have time I will study the prerequisites for the Milnor's paper

if you don't want to learn tikz but still need them arrows, check out quiver. it's super useful for complicated and unconventional diagrams
Learning LaTex has been a way more pleasant experience than I thought it would be this stuff is way simpler than it looks and the results fuck hard
tips for studying math
I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas
1. note taking
some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)
2. active learning
do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions
3. exercises
many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going
4. textbooks and other sources
finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill
5. studying for exams
do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work
6. examples and counterexamples
there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember
7. motivation
and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting
8. studying for exams vs studying longterm
oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped
ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours
Okay I’m currently furious that migraines are often so blindly easy to treat and I had to find this out myself at the age of 26 when I’ve been to a neurologist since I was 11 lol so I’m about to teach you two neat and fast little tricks to deal with pain!
The first is the sternocleidomastoid muscle, or the SCM muscle.
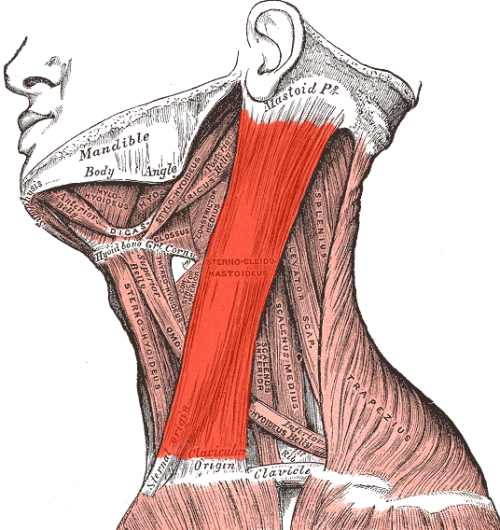
This big red section is responsible for pain around the eye, cheekbone, and jaw, as well as some temple pain. Literally all you have to do is angle your head down a little, angle it away from the side that hurts, and then you can gently pinch and rub that muscle. I find it best to start at the bottom and travel upwards. The relief is so immediate! You can increase pressure as you feel comfortable doing so.
Here is a short and easy video showing this in action
The second is a fast and easy stretch that soothes your vagus nerve, which is the nerve responsible for calming you down. The vagus nerve, for those unfamiliar, is stimulated by deep breathing such as yawning, sighing, singing, or taking a deep breath to calm your anger in a tense situation.
You can stretch this out by sitting up as straight as possible (this does not have to be perfect to work) and interlacing your fingers. Put your hands on the back of your head with your thumbs going down the sides of your neck and, while keeping your face forward, look all the way to one side with just your eyes. Hold that until you feel the urge to breathe deeply or yawn, or until you can tell there’s a change. Then do the same thing on the other side. When you put your arms down, you should clearly be able to turn your head farther in both directions. If the first session doesn’t get rid of your migraine, rest and repeat as many times as necessary. I even get a little fancy with it and roll my eyes up and down along the outer edge sometimes to stretch as much as I can.
If you need a visual here’s a good video on it. I know some of the language they use seems questionable but this is real and simple science and should not be discarded because it’s been adopted by the trendy wellness crowd!
I seriously cannot believe I didn’t hear a word of this from any doctor in my life. Additionally, if you get frequent recurring migraines, you may want to see a dietician. Migraines can be caused by foods containing histamines, lectin, etc. and can also be caused by high blood pressure in specific situations such as exercise, stress, and even sex.
If any of this information helps you I’d love to hear it btw! It’s so so fast and easy to do. Good luck!
-
 londonfag liked this · 2 months ago
londonfag liked this · 2 months ago -
 electronsprotonscroutons reblogged this · 2 months ago
electronsprotonscroutons reblogged this · 2 months ago -
 dexxxtrodna liked this · 2 months ago
dexxxtrodna liked this · 2 months ago -
 fourends reblogged this · 2 months ago
fourends reblogged this · 2 months ago -
 aesofhubris reblogged this · 3 months ago
aesofhubris reblogged this · 3 months ago -
 caranthira reblogged this · 4 months ago
caranthira reblogged this · 4 months ago -
 johnsilva liked this · 5 months ago
johnsilva liked this · 5 months ago -
 wingedsandwichcollector reblogged this · 5 months ago
wingedsandwichcollector reblogged this · 5 months ago -
 macsarcule1 reblogged this · 5 months ago
macsarcule1 reblogged this · 5 months ago -
 maopopo222 reblogged this · 5 months ago
maopopo222 reblogged this · 5 months ago -
 wingedsandwichcollector liked this · 5 months ago
wingedsandwichcollector liked this · 5 months ago -
 carnalreincarnated liked this · 5 months ago
carnalreincarnated liked this · 5 months ago -
 swtfrmx liked this · 5 months ago
swtfrmx liked this · 5 months ago -
 swtfrmx reblogged this · 5 months ago
swtfrmx reblogged this · 5 months ago -
 sensuousnonsense reblogged this · 5 months ago
sensuousnonsense reblogged this · 5 months ago -
 sexartdesigncrime reblogged this · 5 months ago
sexartdesigncrime reblogged this · 5 months ago -
 nonamerat reblogged this · 5 months ago
nonamerat reblogged this · 5 months ago -
 lmaster37 liked this · 5 months ago
lmaster37 liked this · 5 months ago -
 wanderingchronicle reblogged this · 5 months ago
wanderingchronicle reblogged this · 5 months ago -
 ninethousandbees reblogged this · 5 months ago
ninethousandbees reblogged this · 5 months ago -
 ninethousandbees liked this · 5 months ago
ninethousandbees liked this · 5 months ago -
 eremes liked this · 5 months ago
eremes liked this · 5 months ago -
 brazenbell reblogged this · 5 months ago
brazenbell reblogged this · 5 months ago -
 absenceoffield liked this · 5 months ago
absenceoffield liked this · 5 months ago -
 thelastranger liked this · 5 months ago
thelastranger liked this · 5 months ago -
 pleiadesarm liked this · 5 months ago
pleiadesarm liked this · 5 months ago -
 docxie liked this · 5 months ago
docxie liked this · 5 months ago -
 foxglovedforest liked this · 5 months ago
foxglovedforest liked this · 5 months ago -
 wobubling reblogged this · 5 months ago
wobubling reblogged this · 5 months ago -
 throwingbread liked this · 5 months ago
throwingbread liked this · 5 months ago -
 schwimmingly liked this · 5 months ago
schwimmingly liked this · 5 months ago -
 eyes-eyes-eyes-girls-girls-girls liked this · 5 months ago
eyes-eyes-eyes-girls-girls-girls liked this · 5 months ago -
 chiefofboatwatsonstittymug liked this · 5 months ago
chiefofboatwatsonstittymug liked this · 5 months ago -
 s0urcedecay liked this · 5 months ago
s0urcedecay liked this · 5 months ago -
 spacesharkss liked this · 5 months ago
spacesharkss liked this · 5 months ago -
 rbr-seb reblogged this · 5 months ago
rbr-seb reblogged this · 5 months ago -
 janetfraisersmassivestrap reblogged this · 5 months ago
janetfraisersmassivestrap reblogged this · 5 months ago -
 janetfraisersmassivestrap liked this · 5 months ago
janetfraisersmassivestrap liked this · 5 months ago -
 spritznar liked this · 5 months ago
spritznar liked this · 5 months ago -
 zombie-bait liked this · 5 months ago
zombie-bait liked this · 5 months ago -
 perpetually-dehydrated liked this · 5 months ago
perpetually-dehydrated liked this · 5 months ago -
 andrewndrag liked this · 5 months ago
andrewndrag liked this · 5 months ago -
 andrewndrag reblogged this · 5 months ago
andrewndrag reblogged this · 5 months ago -
 leelovesbooksandthemarauders liked this · 5 months ago
leelovesbooksandthemarauders liked this · 5 months ago -
 asushunamir2051 reblogged this · 5 months ago
asushunamir2051 reblogged this · 5 months ago -
 asushunamir2051 liked this · 5 months ago
asushunamir2051 liked this · 5 months ago -
 singing-sorrowless reblogged this · 5 months ago
singing-sorrowless reblogged this · 5 months ago -
 tangleofgold liked this · 5 months ago
tangleofgold liked this · 5 months ago -
 astercrash liked this · 5 months ago
astercrash liked this · 5 months ago

⁕ pure math undergrad ⁕ in love with anything algebraic ⁕
292 posts