Energy Management



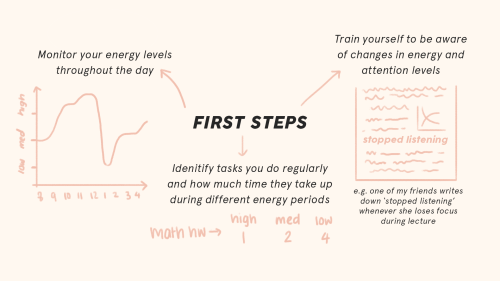
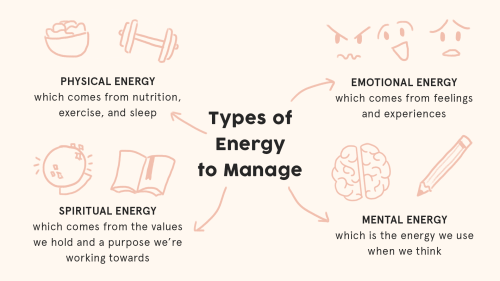
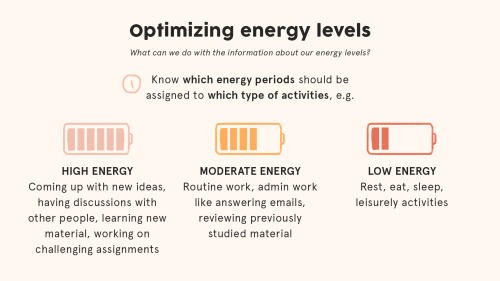




Energy Management
A human-based organization method
click on images for better resolution; images also available here (link to google drive)
Other posts that may be of interest:
Getting stuff done: How to deal with a lack of motivation
Flexible time-blocking: A more breathable way to get things done
The ABCDE Method
More Posts from Bsdndprplplld and Others

5x5 Diamond rule, iterates 1-32



Iterates 40, 48, 56

Iterate 64

Iterate 128
This is a 2D cellular automaton generating a 3D fractal layer by layer. I coded it in Microsoft Excel - each pixel is 1 cell.
See more MSExcel fractals
14 II 2023
so yesterday would be the last of my exams but I decided to retake both the written and the oral part. the grade I would get is 4, so not the highest possible, still pretty good especially for the standards of that course (it's one of the most difficult), but I am not satisfied
it was the professor who suggested I retake the exams, which surprised me, I was mentally prepared to finish being only half-happy about my results and his reactions, strangely enough, inspired me to try harder. he wouldn't offer it if he didn't think I could do better, right?
if he gave me a 5 with my written exam points I would feel like an impostor, because I don't think I am fluent enough with the topics to receive the best grade. to be graded 4 and not being effered the chance to try again would make me feel that it's done, I was just too slow and I can't do anything else to fix it (at least on paper, but we're talking symbolics now) and him giving me a second chance meant to me that he believes in my potential yet doesn't want to give me a participation trophy, instead he made it about earning the reward that I know I deserve
he achieved the aurea mediocritas with this and the most absurd part of it all is that he of all people was to give me this inspiration. half of the students I talk to think that he is pure evil, the majority of the other half think he is an inconsiderate asshole lmao
so in two weeks I'm trying the exam again. in the meantime I will have a party with friends (small – 5 people + my boyfriend's cat) and then I will be grading the math olympiad. afterwards my another grind of algebraic methods shall commence and this time please let me not fuck it up
13 III 2023
I remember putting it in my bio a while ago that I dream of doing actual research one day. well this is already happening, as I mentioned in some post, my advisor found an open question for me to write my thesis about
the progress for now is that I'm done with most of the reading I need to do to tackle it and I'm slowly moving forward with thinking of ideas for the solution (or at least a partial one)

this is what I want to do for the rest of my life: reading papers and trying to write my own ones
ofc I don't know if I manage to solve the problem or achieve anything at all with it but the process itself is fun
other than that I've been catching up with homeworks and assignments from work. fortunately I found an MIT lecture recordings for statistics so hopefully I might not die from boredom

watching probability and stats lectures from MIT has been my relationship's idea of netflix and chill for a while now, gotta cultivate the tradition
the algtop professor asked us to write down a full detailed solution for an exercises we did in class, because the person presenting was unable to explain it so I sent him mine


I don't know yet if it's correct but I'm pretty sure it is. I wrote this down partly because who doesn't want extra points and partly because I didn't have a chance to present it, the person who did was faster
I like how my life is right now, I want to keep it that way
My favourite fucked up math fact™ is the Sharkovskii theorem:
For any continuous function f: [a,b] -> [a,b], if there exists a periodic point of order 3 (i.e. f(f(f(x))) = x for some x in [a,b] and not f(x) = x or f²(x) = x), then there exists a periodic point of ANY order n.¹
Yes you read that right. If you can find a point of order 3 then you can be sure that there is a point of order 4, 5, or even 142857 in your interval. The assumption is so innocent but I cannot understate how ridiculous the result is.²
For a (relatively) self-contained proof, see this document (this downloads a pdf).
(footnotes under read more)
¹ The interval does not have to be closed, but it should be connected. (a,b), (a,b] and [a,b) all work.
² Technically the result is even stronger! The natural numbers admit a certain ordering called the Sharkovskii ordering which starts with the odd primes 3 > 5 > 7 > ... , then doubles of primes, then quadruples of primes and so forth until you get no more primes left, ending the ordering in 2³ > 2² > 2. Sharkovskii's theorem actually says that if you have a periodic point of order k, then you have periodic points of any order less than k in the Sharkovskii ordering. It is frankly ridiculous how somehow prime numbers make their way into this mess.
http://proof.ucalgaryblogs.ca/
This is the best resource for studying math that I've found in a while! It's 300+ pages of flawed/incorrect proofs on topics including logic, analysis, and linear algebra. Each flawed proof is followed by a classification of its errors, and a corrected version.
oh i just saw, congrats on the bachelors!! im still in calc 3, i thought itd be less mundane but it is actually killing now to the point where i cant even open our stewart text. all my friends in decent math programs are doing more fun and general versions this course. i just cant wait to not use this awful book anymore (all our work is based on the books problems and methodology). all this is to say your progress is inspiring. hopefully i get to a point where i can also be having fun around structures and such, i just have to finish grinding through the filter of "do a bunch of this and don't worry about what it really means, btw good luck problem solving on your exams with 0 neither provided intuition nor rigor". i hope blogs like this stick around!
thank you for the nice message!
I'm so sorry to hear that this is how they teach you math, something like this takes away all pleasure and satisfaction. I didn't have calc 3 as such at my university, we would generally focus on theory and understanding from the start. however, we did have some courses where the mindset was like you just described and it was torture. I hope it changes for you soon so that you can finally enjoy some beautiful math!

Pick a point inside a triangle and drop perpendicular projections onto the sides. These define another triangle. Repeat, with the same point but within the new triangle. Do the same thing once more. The fourth triangle now has the same angles as the first one, although it’s much smaller and it’s rotated.
Theory Time
The reason endermen don’t like it when you look at them is because they communicate telepathically with one another by locking eyes! Humans are absolutely not designed to do this so when we look at them we are accidentally projecting all of our thoughts into them at the same time and it hurts :(
uhh probably the worst math feeling is when you're so excited about proving something and you talk about it to someone who does math with you and they say oh but it's trivial

“A lot of math grad school is reading books and papers and trying to understand what’s going on. The difficulty is that reading math is not like reading a mystery thriller, and it’s not even like reading a history book or a New York Times article.
The main issue is that, by the time you get to the frontiers of math, the words to describe the concepts don’t really exist yet. Communicating these ideas is a bit like trying to explain a vacuum cleaner to someone who has never seen one, except you’re only allowed to use words that are four letters long or shorter.
What can you say?
“It is a tool that does suck up dust to make what you walk on in a home tidy.”
That’s certainly better than nothing, but it doesn’t tell you everything you might want to know about a vacuum cleaner. Can you use a vacuum cleaner to clean bookshelves? Can you use a vacuum cleaner to clean a cat? Can you use a vacuum cleaner to clean the outdoors?
The authors of the papers and books are trying to communicate what they’ve understood as best they can under these restrictions, and it’s certainly better than nothing, but if you’re going to have to work with vacuum cleaners, you need to know much more.
Fortunately, math has an incredibly powerful tool that helps bridge the gap. Namely, when we come up with concepts, we also come up with very explicit symbols and notation, along with logical rules for manipulating them. It’s a bit like being handed the technical specifications and diagrams for building a vacuum cleaner out of parts.
The upside is that now you (in theory) can know 100% unambiguously what a vacuum cleaner can or cannot do. The downside is that you still have no clue what the pieces are for or why they are arranged the way they are, except for the cryptic sentence, “It is a tool that does suck up dust to make what you walk on in a home tidy.”
OK, so now you’re a grad student, and your advisor gives you an important paper in the field to read: “A Tool that does Suck Dust.” The introduction tells you that “It is a tool that does suck up dust to make what you walk on in a home tidy,” and a bunch of other reasonable but vague things. The bulk of the paper is technical diagrams and descriptions of a vacuum cleaner. Then there are some references: “How to use air flow to suck up dust.” “How to use many a coil of wire to make a fan spin very fast.” “What you get from the hole in the wall that has wire in it.”
So, what do you do? Technically, you sit at your desk and think. But it’s not that simple. First, you’re like, lol, that title almost sounds like it could be sexual innuendo. Then you read the introduction, which pleasantly tells you what things are generally about, but is completely vague about the important details.
Then you get to the technical diagrams and are totally confused, but you work through them piece by piece. You redo many of the calculations on your own just to double check that you’ve really understood what’s going on. Sometimes, the calculations that you redo come up with something stupid, and then you have to figure out what you’ve understood incorrectly, and then reread that part of the technical manual to figure things out. Except sometimes there was a typo in the paper, so that’s what screwed things up for you.
After a while, things finally click, and you finally understand what a vacuum cleaner is. In fact, you actually know much more: You’ve now become one of the experts on vacuum cleaners, or at least on this particular kind of vacuum cleaner, and you know a good fraction of the details on how it works. You’re feeling pretty proud of yourself, even though you’re still a far shot from your advisor: They understand all sorts of other kinds of vacuum cleaners, even Roombas, and, in addition to their work on vacuum cleaners, they’re also working on a related but completely different project about air conditioning systems.
You are filled with joy that you can finally talk on par with your advisor, at least on this topic, but there is a looming dark cloud on the horizon: You still need to write a thesis.
So, you think about new things that you can do with vacuum cleaners. So, first, you’re like: I can use a vacuum cleaner to clean bookshelves! That’d be super-useful! But then you do a Google Scholar search and it turns out that someone else did that like ten years ago.
OK, your next idea: I can use a vacuum cleaner to clean cats! That’d also be super-useful. But, alas, a bit more searching in the literature reveals that someone tried that, too, but they didn’t get good results. You’re a confident young grad student, so you decide that, armed with some additional techniques that you happen to know, you might fix the problems that the other researcher had and get vacuuming cats to work. You spend several months on it, but, alas, it doesn’t get you any further.
OK, so then, after more thinking and doing some research on extension cords, you think it would be feasible to use a vacuum cleaner to clean the outdoors. You look in the literature, and it turns out that nobody’s ever thought of doing that! You proudly tell this idea to your advisor, but they do some back of the envelope calculations that you don’t really understand and tell you that vacuuming the outdoors is unlikely to be very useful. Something about how a vacuum cleaner is too small to handle the outdoors and that we already know about other tools that are much better equipped for cleaning streets and such.
This goes on for several years, and finally you write a thesis about how if you turn a vacuum cleaner upside-down and submerge the top end in water, you can make bubbles!
Your thesis committee is unsure of how this could ever be useful, but it seems pretty cool and bubbles are pretty, so they think that maybe something useful could come out of it eventually. Maybe.
And, indeed, you are lucky! After a hundred years or so, your idea (along with a bunch of other ideas) leads to the development of aquarium air pumps, an essential tool in the rapidly growing field of research on artificial goldfish habitats. Yay!”
-
 lovelight-magic liked this · 3 weeks ago
lovelight-magic liked this · 3 weeks ago -
 demonhen reblogged this · 3 weeks ago
demonhen reblogged this · 3 weeks ago -
 pickyourpoisonmydear liked this · 3 weeks ago
pickyourpoisonmydear liked this · 3 weeks ago -
 coldcheesecakemilkshake liked this · 3 weeks ago
coldcheesecakemilkshake liked this · 3 weeks ago -
 astudiouspeach reblogged this · 1 month ago
astudiouspeach reblogged this · 1 month ago -
 everchangingwithsentimentality liked this · 1 month ago
everchangingwithsentimentality liked this · 1 month ago -
 learningtoletgo reblogged this · 1 month ago
learningtoletgo reblogged this · 1 month ago -
 muhtesemz liked this · 1 month ago
muhtesemz liked this · 1 month ago -
 cannibology liked this · 1 month ago
cannibology liked this · 1 month ago -
 noxernia reblogged this · 1 month ago
noxernia reblogged this · 1 month ago -
 lavisnthere liked this · 1 month ago
lavisnthere liked this · 1 month ago -
 naistudylab reblogged this · 1 month ago
naistudylab reblogged this · 1 month ago -
 noxernia reblogged this · 1 month ago
noxernia reblogged this · 1 month ago -
 fabergenestegg reblogged this · 1 month ago
fabergenestegg reblogged this · 1 month ago -
 fabergenestegg liked this · 1 month ago
fabergenestegg liked this · 1 month ago -
 noxernia liked this · 2 months ago
noxernia liked this · 2 months ago -
 peach-ice-tea-and-mint liked this · 2 months ago
peach-ice-tea-and-mint liked this · 2 months ago -
 joystudiesss reblogged this · 2 months ago
joystudiesss reblogged this · 2 months ago -
 brittsdiary reblogged this · 2 months ago
brittsdiary reblogged this · 2 months ago -
 brittsdiary liked this · 2 months ago
brittsdiary liked this · 2 months ago -
 girlwithnojob25 liked this · 2 months ago
girlwithnojob25 liked this · 2 months ago -
 artemis-academic liked this · 2 months ago
artemis-academic liked this · 2 months ago -
 dreamcatcherltn liked this · 2 months ago
dreamcatcherltn liked this · 2 months ago -
 blewahismejik liked this · 2 months ago
blewahismejik liked this · 2 months ago -
 peachflavoredstar liked this · 2 months ago
peachflavoredstar liked this · 2 months ago -
 somegrrrl liked this · 2 months ago
somegrrrl liked this · 2 months ago -
 o2studies reblogged this · 2 months ago
o2studies reblogged this · 2 months ago -
 o2studies liked this · 2 months ago
o2studies liked this · 2 months ago -
 bitchybananabird reblogged this · 2 months ago
bitchybananabird reblogged this · 2 months ago -
 thelittolpinkstudent reblogged this · 2 months ago
thelittolpinkstudent reblogged this · 2 months ago -
 thelittolpinklady liked this · 2 months ago
thelittolpinklady liked this · 2 months ago -
 goglimarshmallowme liked this · 2 months ago
goglimarshmallowme liked this · 2 months ago -
 thedavesofourlives liked this · 2 months ago
thedavesofourlives liked this · 2 months ago -
 adhdhd reblogged this · 2 months ago
adhdhd reblogged this · 2 months ago -
 math-markers reblogged this · 2 months ago
math-markers reblogged this · 2 months ago -
 hellbentsunday liked this · 2 months ago
hellbentsunday liked this · 2 months ago -
 oukamomochi reblogged this · 2 months ago
oukamomochi reblogged this · 2 months ago -
 dancinglikebutterfly reblogged this · 2 months ago
dancinglikebutterfly reblogged this · 2 months ago -
 rabbitstudy reblogged this · 2 months ago
rabbitstudy reblogged this · 2 months ago -
 rabbitstudy liked this · 2 months ago
rabbitstudy liked this · 2 months ago -
 kthbaequeen liked this · 2 months ago
kthbaequeen liked this · 2 months ago -
 zsandpearls reblogged this · 3 months ago
zsandpearls reblogged this · 3 months ago -
 yearsofbear reblogged this · 3 months ago
yearsofbear reblogged this · 3 months ago -
 autistictomato liked this · 3 months ago
autistictomato liked this · 3 months ago -
 bobrisky liked this · 3 months ago
bobrisky liked this · 3 months ago -
 bemagicshell liked this · 4 months ago
bemagicshell liked this · 4 months ago -
 organised-kitty liked this · 4 months ago
organised-kitty liked this · 4 months ago -
 ifollowmagicalrivers liked this · 5 months ago
ifollowmagicalrivers liked this · 5 months ago

⁕ pure math undergrad ⁕ in love with anything algebraic ⁕
292 posts