Tag Yourself I’m The Data Noodle

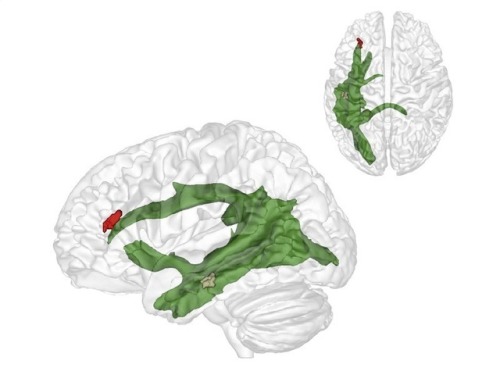
(Image caption: The maturation of fibres of a brain structure called the arcuate fascicle (green) between the ages of three and four years establishes a connection between two critical brain regions: a region (brown) at the back of the temporal lobe that supports adults thinking about others and their thoughts, and a region (red) in the frontal lobe that is involved in keeping things at different levels of abstraction and, therefore, helps us to understand what the real world is and what the thoughts of others are. Credit: © MPI CBS)

The importance of relating to others: why we only learn to understand other people after the age of four

When we are around four years old we suddenly start to understand that other people think and that their view of the world is often different from our own. Researchers in Leiden and Leipzig have explored how that works. Publication in Nature Communications on 21 March.

At around the age of four we suddenly do what three-year-olds are unable to do: put ourselves in someone else’s shoes. Researchers at the Max Planck Institute for Human Cognitive and Brain Sciences (MPI CBS) in Leipzig and at Leiden University have shown how this enormous developmental step occurs: a critical fibre connection in the brain matures. Senior researcher and Leiden developmental psychologist Nikolaus Steinbeis, co-author of the article, took part in the research. Lead author, PhD candidate Charlotte Grosse-Wiesmann, worked under his supervision.

Little Maxi

If you tell a 3-year-old child the following story of little Maxi, they will most probably not understand: Maxi puts his chocolate on the kitchen table, then goes to play outside. While he is gone, his mother puts the chocolate in the cupboard. Where will Maxi look for his chocolate when he comes back? A 3-year-old child will not understand why Maxi would be surprised not to find the chocolate on the table where he left it. It is only by the age of 4 years that a child will correctly predict that Maxi will look for his chocolate where he left it and not in the cupboard where it is now.

Theory of Mind

The researchers observed something similar when they showed a 3-year-old child a chocolate box that contained pencils instead of chocolates. When the child was asked what another child would expect to be in the box, they answered “pencils”, although the other child would not know this. Only a year later, around the age of four years, however, will they understand that the other child had hoped for chocolates. Thus, there is a crucial developmental breakthrough between three and four years: this is when we start to attribute thoughts and beliefs to others and to understand that their beliefs can be different from ours. Before that age, thoughts don’t seem to exist independently of what we see and know about the world. That is, this is when we develop a Theory of Mind.

Independent development

The researchers have now discovered what is behind this breakthrough. The maturation of fibres of a brain structure called the arcuate fascicle between the ages of three and four years establishes a connection between two critical brain regions: a region at the back of the temporal lobe that supports adult thinking about others and their thoughts, and a region in the frontal lobe that is involved in keeping things at different levels of abstraction and, therefore, helps us to understand what the real world is and what the thoughts of others are. Only when these two brain regions are connected through the arcuate fascicle can children start to understand what other people think. This is what allows us to predict where Maxi will look for his chocolate. Interestingly, this new connection in the brain supports this ability independently of other cognitive abilities, such as intelligence, language ability or impulse control.

---

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

---

Are humans the new supercomputer?

The saying of philosopher René Descartes of what makes humans unique is beginning to sound hollow. ‘I think – therefore soon I am obsolete’ seems more appropriate. When a computer routinely beats us at chess and we can barely navigate without the help of a GPS, have we outlived our place in the world? Not quite. Welcome to the front line of research in cognitive skills, quantum computers and gaming.

Today there is an on-going battle between man and machine. While genuine machine consciousness is still years into the future, we are beginning to see computers make choices that previously demanded a human’s input. Recently, the world held its breath as Google’s algorithm AlphaGo beat a professional player in the game Go—an achievement demonstrating the explosive speed of development in machine capabilities.

But we are not beaten yet - human skills are still superior in some areas. This is one of the conclusions of a recent study by Danish physicist Jacob Sherson, published in the prestigious science journal Nature.

”It may sound dramatic, but we are currently in a race with technology—and steadily being overtaken in many areas. Features that used to be uniquely human are fully captured by contemporary algorithms. Our results are here to demonstrate that there is still a difference between the abilities of a man and a machine,” explains Jacob Sherson.

At the interface between quantum physics and computer games, Sherson and his research group at Aarhus University have identified one of the abilities that still makes us unique compared to a computer’s enormous processing power: our skill in approaching problems heuristically and solving them intuitively. The discovery was made at the AU Ideas Centre CODER, where an interdisciplinary team of researchers work to transfer some human traits to the way computer algorithms work. 


Quantum physics holds the promise of immense technological advances in areas ranging from computing to high-precision measurements. However, the problems that need to be solved to get there are so complex that even the most powerful supercomputers struggle with them. This is where the core idea behind CODER—combining the processing power of computers with human ingenuity—becomes clear. 


Our common intuition Like Columbus in QuantumLand, the CODER research group mapped out how the human brain is able to make decisions based on intuition and accumulated experience. This is done using the online game “Quantum Moves”. Over 10,000 people have played the game that allows everyone contribute to basic research in quantum physics.

"The map we created gives us insight into the strategies formed by the human brain. We behave intuitively when we need to solve an unknown problem, whereas for a computer this is incomprehensible. A computer churns through enormous amounts of information, but we can choose not to do this by basing our decision on experience or intuition. It is these intuitive insights that we discovered by analysing the Quantum Moves player solutions,” explains Jacob Sherson. 


The laws of quantum physics dictate an upper speed limit for data manipulation, which in turn sets the ultimate limit to the processing power of quantum computers—the Quantum Speed ​​Limit. Until now a computer algorithm has been used to identify this limit. It turns out that with human input researchers can find much better solutions than the algorithm.

"The players solve a very complex problem by creating simple strategies. Where a computer goes through all available options, players automatically search for a solution that intuitively feels right. Through our analysis we found that there are common features in the players’ solutions, providing a glimpse into the shared intuition of humanity. If we can teach computers to recognise these good solutions, calculations will be much faster. In a sense we are downloading our common intuition to the computer” says Jacob Sherson.

And it works. The group has shown that we can break the Quantum Speed Limit by combining the cerebral cortex and computer chips. This is the new powerful tool in the development of quantum computers and other quantum technologies.

We are the new supercomputer

Science is often perceived as something distant and exclusive, conducted behind closed doors. To enter you have to go through years of education, and preferably have a doctorate or two. Now a completely different reality is materialising. 


In recent years, a new phenomenon has appeared—citizen science breaks down the walls of the laboratory and invites in everyone who wants to contribute. The team at Aarhus University uses games to engage people in voluntary science research. Every week people around the world spend 3 billion hours playing games. Games are entering almost all areas of our daily life and have the potential to become an invaluable resource for science.

“Who needs a supercomputer if we can access even a small fraction of this computing power? By turning science into games, anyone can do research in quantum physics. We have shown that games break down the barriers between quantum physicists and people of all backgrounds, providing phenomenal insights into state-of-the-art research. Our project combines the best of both worlds and helps challenge established paradigms in computational research,” explains Jacob Sherson.

The difference between the machine and us, figuratively speaking, is that we intuitively reach for the needle in a haystack without knowing exactly where it is. We ‘guess’ based on experience and thereby skip a whole series of bad options. For Quantum Moves, intuitive human actions have been shown to be compatible with the best computer solutions. In the future it will be exciting to explore many other problems with the aid of human intuition.

"We are at the borderline of what we as humans can understand when faced with the problems of quantum physics. With the problem underlying Quantum Moves we give the computer every chance to beat us. Yet, over and over again we see that players are more efficient than machines at solving the problem. While Hollywood blockbusters on artificial intelligence are starting to seem increasingly realistic, our results demonstrate that the comparison between man and machine still sometimes favours us. We are very far from computers with human-type cognition,” says Jacob Sherson and continues:

“Our work is first and foremost a big step towards the understanding of quantum physical challenges. We do not know if this can be transferred to other challenging problems, but it is definitely something that we will work hard to resolve in the coming years.”

---

List of Free Science Books

Here’s an alphabetical list of all available free books. Note that many of the links will bring you to an external page, usually with more info about the book and the download links. Also, the links are updated as frequently as possible, however some of them might be broken. Broken links are constantly being fixed. In case you want to report a broken link, or a link that violates copyrights, use the contact form.

A

A Beginner’s Guide to Mathematica

A Brief Introduction to Particle Physics

A First Course in General Relativity

A New Astronomy

A No-Nonsense Introduction to General Relativity

A Popular History of Astronomy During the Nineteenth Century, Fourth Edition

A Review of General Chemistry

A Simple Guide to Backyard Astronomy

A Text Book for High School Students Studying Physics

A Tour of Triangle Geometry

About Life: Concepts in Modern Biology

Acoustic Emission

Adaptive Control

Advanced Calculus

Advanced Learning

Advanced Mathematics for Engineers

Advanced Microwave Circuits and Systems

Advanced Technologies

Advances in Computer Science and IT

Advances in Evolutionary Algorithms

Advances in Geoscience and Remote Sensing

Advances in Haptics

Advances in Human Computer Interaction

Age of Einstein

Aging by Design

AMPL:  A Modeling Language for Mathematical Programming

An Introduction to Elementary Particles

An Introduction to Higher Mathematics

An Introduction to Many Worlds in Quantum Computation

An Introduction to Mathematical Reasoning

An Introduction to Mathematics

An Introduction to Proofs and the Mathematical Vernacular

An Introduction to Relativistic Quantum Mechanics

Analysis 1 (Tao T)

Analysis 2 (Tao T)

Analytic Functions

Astronomical Discovery

Astronomy for Amateurs

Astronomy Today

Astronomy with an Opera-Glass

Automation and Robotics

B

Basic Algebra, Topology and Differential Calculus

Basic Concepts of Mathematics

Basic Concepts of Thermodynamics

Basic Concepts of Thermodynamics Chapter 1

Basic Ideas in Chemistry

Basic Math: Quick Reference eBook

Basic Mathematics for Astronomy

Basic Physics

Basic Positional Astronomy

Basic Principles of Classical and Statistical Thermodynamics

Basic Principles of Physics

Basics of Physics

Beginner’s Botany

Biochemistry

Biochemistry (practice book)

Biology

Board Notes for Particle Physics

Book of Proof

C

Calculus

Calculus Based Physics

Celestial Navigation, Elementary Astronomy, Piloting

Circuit QED — Lecture Notes

Classical Dynamics

Classical Geometry

Classical Mechanics

Climate Models

Collaborative Statistics

College Algebra

Complex Analysis

Computational Geometry

Computational Introduction to Number Theory and Algebra

Computational Physics with Python

Conceptual Physics

Consistent Quantum Theory

Cook-Book Of Mathematics

College Physics

Crude Oil Emulsions- Composition Stability and Characterization

Curiosities of the Sky

D

Decoherence: Basic Concepts and Their Interpretation

Do We Really Understand Quantum Mechanics?

Differential Equations

Diophantine Analysis

Discover Physics

Dr. Donald Luttermoser’s Physics Notes

Dynamics and Relativity

E

Earthquake Research and Analysis

Earthquake-Resistant Structures – Design, Assessment and Rehabilitation

Einstein for Everyone

Electromagnetic Field Theory

Elementary Mathematical Astronomy

Elementary Linear Algebra

Elementary Particle Physics in a Nutshell

Elementary Particles in Physics

Elements of Astrophysics

Embedded Systems – Theory and Design Methodology

Encyclopaedia of Mathematics

Encyclopedia of Astrophysics

Engineering Mathematics 1

Engineering Mathematics with Tables

Essential Engineering Mathematics

Essential Physics

Exoplanet Observing for Amateurs

Experimental Particle Physics

F

Fields

Foundations of Nonstandard Analysis

Frequently Asked Questions about Calendars

Fundamental Concepts of Mathematics

Fundamentals of Analysis (Chen W.W.L)

Further Mathematical Methods

Fusion Physics

G

General Chemistry

General Relativity

General Relativity

Geometric Asymptotics

Geometry and Group Theory

Geometry and Topology

Geometry Formulas and Facts

Geometry Study Guide

Geometry, Topology and Physics

Geometry, Topology, Localization and Galois Symmetry

Great Astronomers

H

Handbook of Formulae and Physical Constants

High School Mathematics Extensions

Higher Mathematics for Engineers and Physicists

History of Astronomy

Homeomorphisms in Analysis

How to Use Experimental Data to Compute the Probability of Your Theory

I

Intelligent Systems

Intrinsic Geometry of Surfaces

Introduction to Astronomy and Cosmology

Introduction to Cancer Biology

Introduction to Chemistry

Introduction to Cosmology

Introduction to Elementary Particles

Introduction to General Relativity

Introduction To Finite Mathematics

Introduction to Particle Physics Notes

Introduction to PID Controllers

Introduction to Quantum Mechanics with Applications to Chemistry

Introduction to Quantum Noise, Measurement and Amplification

Introduction to Social Network Methods

Introduction to String Field Theory

Introduction to the Time Evolution of Open Quantum Systems

Introduction to Quantum Mechanics

Introductory Computational Physics

Introductory Physics 1

Introductory Physics 2

K

Kinetic Theory

L

Laboratory Manual for Introductory Physics

Laws of Physics

Learn Physics Today

Lecture Notes in Discrete Mathematics

Lecture Notes in Quantum Mechanics

Lecture Notes in Nuclear and Particle Physics

Lecture Notes in Particle Physics

Lecture Notes on General Relativity

Lectures on Astronomy, Astrophysics, and Cosmology

Lectures on Particle Physics

Lectures on Riemann Zeta-Function

Light and Matter

M

Mag 7 Star Atlas Project

Many Particle Physics

Math Alive

Mathematical Analysis I(Zakon E)

Mathematical Biology

Mathematical Methods

Mathematical Methods 1

Mathematical Methods for Physical Sciences

Mathematical Methods of Engineering Analysis

Mathematics, Basic Math and Algebra

Mathematics for Computer Science

Mathematics for Computer Science

Mathematics for Computer Scientists

Mathematics For Engineering Students

Mathematics Formulary

Motion Mountain

Music: A Mathematical Offering

Mysteries of the Sun

N

Natural Disasters

New Frontiers in Graph Theory

Noise Control, Reduction and Cancellation Solutions in Engineering

Nondestructive Testing Methods and New Applications

Nonlinear Optics

Notes on Coarse Geometry

Notes on Elementary Particle Physics

Notes on Quantum Mechanics

O

Observing the Sky from 30S

On Particle Physics

Operating Systems: Three Easy Pieces

P

Particle Physics Course Univ. Cape Town

Particle Physics Lecture Notes

People’s Physics Book

Perspectives in Quantum Physics: Epistemological, Ontological and Pedagogical

Photons, Schmotons

Physics Lectures

Physics Tutorials

Physics Study Guides

Pioneers of Science

Practical Astronomy

Practical Astronomy for Engineers

Preparing for College Physics

Primer Of Celestial Navigation

Principal Component Analysis – Multidisciplinary Applications

Publications of the Astronomical Society of the Pacific Volume 1

Q

Quantum Dissipative Systems

Quantum Field Theory

Quantum Fluctuations

Quantum Information Theory

Quantum Magnetism

Quantum Mechanics

Quantum Mechanics

Quantum Mechanics: A Graduate Course

Quantum Mechanics: An Intermediate Level Course

Quantum Notes

Quantum Physics Notes

Quantum Theory of Many-Particle Systems

Quantum Transients

R

Recreations in Astronomy

Relativistic Quantum Dynamics

Relativity: The Special and General Theory

Review of Basic Mathematics

Riemann Surfaces, Dynamics and Geometry Course Notes

S

Short History of Astronomy

Sintering of Ceramics – New Emerging Techniques

Solitons

Some Basic Principles from Astronomy

Special Relativity

Spherical Astronomy

Star-Gazer’s Hand-Book

Statistical Physics

Street-Fighting Mathematics

String Theory

Structures of Life

Supernova Remnants: The X-ray Perspective

Superspace: One Thousand and One Lessons in Supersymmetry

System of Systems

T

The Astrobiology Primer: An Outline of General Knowledge

The Astronomy and the Bible

The Astronomy of the Bible: An Elementary Commentary on the Astronomical References of Holy Scripture

The Basic Paradoxes of Statistical Classical Physics and Quantum Mechanics

The Beginning and the End

The Beginning and the End of the Universe

The Complete Idiot’s Guide to the Sun

The Convenient Setting of Global Analysis

The Eightfold Way: The Beauty of Klein’s Quartic Curve

The General Theory of Relativity

The Geology of Terrestrial Planets

The Geometry of the Sphere

The Handbook of Essential Mathematics

The Moon: A Full Description and Map of its Principal Physical Features

The Open Agenda

The Origin of Mass in Particle Physics

The Particle Detector Brief Book

The Physics Hypertextbook

The Physics of Quantum Mechanics

The Planet Mars

The Small n Problem in High Energy Physics

The Story of Eclipses

The Story of the Heavens

The Structure of Life

The Wonder Book of Knowledge

The World According to the Hubble Space Telescope

The Zij as-Sanjari of Gregory Chioniades (June 27, 2009)

Three Dimensional Geometry

U

Understanding Physics

Unfolding the Labyrinth

Utility of Quaternions in Physics

Uses of Astronomy

---

The Graduate, 1967.

---

Oval Eggs

The word egg was a borrowing from Old Norse egg, replacing the native word ey (plural eyren) from Old English ǣġ, plural ǣġru.  Like “children” and “kine” (obsolete plural of cow), the plural ending -en was added redundantly to the plural form in Middle English.  As with most borrowings from Old Norse, this showed up first in northern dialects of English, and gradually moved southwards, so that for a while, ey and egg were used in different parts of England.

In 1490, when William Caxton printed the first English-language books, he wrote a prologue to his publication of Eneydos (Aeneid in contemporary English) in which he discussed the problems of choosing a dialect to publish in, due to the wide variety of English dialects that existed at the time.  This word was a specific example he gave.  He told a story about some merchants from London travelling down the Thames and stopping in a village in Kent 

And one of theym… cam in to an hows and axed for mete and specyally he axyd after eggys, and the goode wyf answerde that she could speke no Frenshe. And the marchaunt was angry, for he also coude speke no Frenshe, but wolde have hadde egges; and she understode hym not. And thenne at laste a-nother sayd that he wolde have eyren. Then the good wyf sayd that she understod hym wel. Loo, what sholde a man in thyse dayes now wryte, egges, or eyren? Certaynly it is hard to playse every man, by-cause of dyversite and chaunge of langage.

The merchant in this story was only familiar with the word egg, while the woman only knew ey, and the confusion was only resolved by someone who knew both words.  Indeed, the woman in the story was so confused by this unfamiliar word egg that she assumed it must be a French word!  The word “meat” (or “mete” as Caxton spelled it) was a generic word for “food” at the time.

The word ey may also survive in the term Cockney, thought to derive from the Middle English cocken ey (”cock’s egg”), a term given to a small misshapen egg, and applied by rural people to townspeople

Both egg and ey derived from the same Proto-Germanic root, *ajją, which apparently had a variant *ajjaz in West Germanic.  This Proto-Germanic form in turn derived from Proto-Indo-European *h2ōwyóm.  In Latin, this root became ōvum, from which the adjective ōvalis meaning “egg-shaped”, was derived.  Ōvum itself was borrowed into English in the biological sense of the larger gamete in animals, while ōvalis is the source of oval.

The PIE root is generally though to derive from the root *h2éwis, “bird”, which is the source of Latin avis “bird”, source of English terms such as aviation.  This word may also be related to *h2ówis “sheep”, which survived in English as ewe.  One theory is that they were both derived from a root meaning something like “to dress”, “to clothe”, with bird meaning “one who is clothed [in feathers]” and sheep meaning “one who clothes [by producing wool]”.

---

The song “It’s a long way to Tipperary” was enormously popular in New Zealand as a sound recording sung by Stanley Kirkby, with shops advertising new arrivals of stock from overseas in early 1915. At the same time, a film of the same title was also being shown in cinemas, and sheet music for an orchestral arrangement was available at the “Golden Horn” music store in Vivian Street Wellington. Copies of this Maori postcard with its “Tipirere “ translation were handed out to members of the 2nd Maori Contingent of the New Zealand Expeditionary Force after they marched through the streets of Wellington on Saturday 16 September 1915 (See Evening Post, 20 September 1915, page 8).

[Postcard]. Tipirere. N.Z.M.E.C. Hokowhitu-a-Tu. [ca 1915].    

Eph-B-POSTCARD-Vol-12-003-btm

---

Meet the orchid mantis.

Orchid mantises—particularly juveniles—seem aptly named. They’re predominantly white with pink or yellow accents, similar to some orchids and other flowers, and their four hind legs are lobed, like petals. But if you search for an exact floral counterpart, as behavioral ecologist James O’Hanlon did, you probably won’t find one. “I spent forever looking for a flower that they look just like,” he says, to no avail.

As it turns out, rather than mimicking one floral species, the insect instead may embody a “generic or an average type of flower” in order to attract bees and other pollinating insects as prey.

What’s more, as far as O’Hanlon can tell, it’s the only animal on record that “takes on the guise of a whole flower blossom” as a predatory strategy. 

Learn more here.

---

I am pretty sure that this cannot be true because I saw an ad from the corn industry that said high fructose corn syrup is good for you…

Fructose alters hundreds of brain genes, which can lead to a wide range of diseases

A range of diseases – from diabetes to cardiovascular disease, and from Alzheimer’s disease to attention deficit hyperactivity disorder – are linked to changes to genes in the brain. A new study by UCLA life scientists has found that hundreds of those genes can be damaged by fructose, a sugar that’s common in the Western diet, in a way that could lead to those diseases.

However, the researchers discovered good news as well: An omega-3 fatty acid known as docosahexaenoic acid, or DHA, seems to reverse the harmful changes produced by fructose.

“DHA changes not just one or two genes; it seems to push the entire gene pattern back to normal, which is remarkable,” said Xia Yang, a senior author of the study and a UCLA assistant professor of integrative biology and physiology. “And we can see why it has such a powerful effect.”

Qingying Meng, Zhe Ying, Emily Noble, Yuqi Zhao, Rahul Agrawal, Andrew Mikhail, Yumei Zhuang, Ethika Tyagi, Qing Zhang, Jae-Hyung Lee, Marco Morselli, Luz Orozco, Weilong Guo, Tina M. Kilts, Jun Zhu, Bin Zhang, Matteo Pellegrini, Xinshu Xiao, Marian F. Young, Fernando Gomez-Pinilla, Xia Yang. Systems Nutrigenomics Reveals Brain Gene Networks Linking Metabolic and Brain Disorders. EBioMedicine, 2016; DOI: 10.1016/j.ebiom.2016.04.008

Americans get most of their fructose in foods that are sweetened with high-fructose corn syrup, an inexpensive liquid sweetener made from corn starch, and from sweetened drinks, syrups, honey and desserts. The Department of Agriculture estimates that Americans consumed an average of about 27 pounds of high-fructose corn syrup in 2014.  Credit: © AlenKadr / Fotolia

---

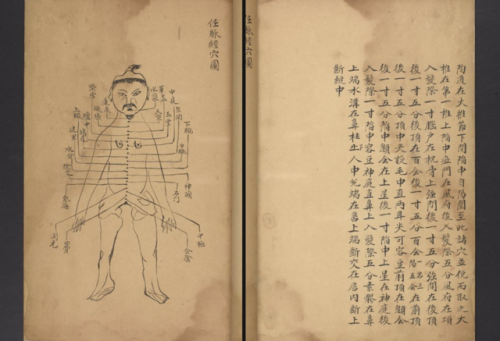
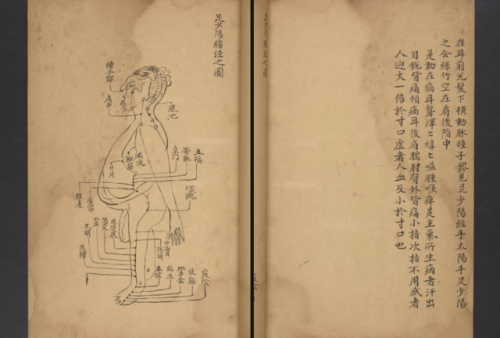
This week, we’re taking a look at manuscripts having to do with health, medicine, and human physiology specifically focusing on how bodies are displayed in manuscript illuminations or diagrams across different cultures.

LJS 389 shown above, is a 14th century Chinese treatise on the anatomy, physiology, and pathology of blood vessels titled Shi si jing fa hui. The manuscript is made from bamboo paper and the diagrams and kaishu script are written with black ink. Focus on the diagrams of the bodies and stay tuned this week to see not only how the details and forms of these depictions change from culture to culture, but also the mediums with which these manuscripts are created.

The full LJS 389 manuscript filled with more diagrams can be found on Openn: http://openn.library.upenn.edu/Data/0001/html/ljs389.html

and Penn In Hand: http://hdl.library.upenn.edu/1017/d/medren/4824235

---