1.8 M Width House By YUUA Architects And Associates

Marine biology basics: a reading list

Someone recently asked me to “explain to me the basics of marine biology“ and I didn’t even know where to begin because that’s a HUGE topic with so much interesting stuff to think about. I asked some of my fellow scientists on twitter and we put together a list of good reading and watching to get an overview of what marine biology is all about. This list is broken down by ages. Comment with any more suggestions and I’ll add them!

Kids:

1)National Geographic Kids, Really Wild Animals, Deep Sea Dive (recommended by @DrKatfish on twitter) I watched this video when I was a kid and have been hooked on cephalopods ever since. If you listened to me on NPR’s Science Friday, this was the video I was talking about!

2) The Magic Schoolbus- on the ocean floor (recommended by @easargent184 and @mirandaRHK on twitter)

Amazon link: https://www.amazon.com/Magic-School-Bus-Ocean-Floor/dp/0590414313#reader_0590414313

3) Ocean Sunlight- How tiny plants feed the seas (recommended by @ColemanLab on twitter)

Amazon link:https://www.amazon.com/Ocean-Sunlight-Tiny-Plants-Feed/dp/0545273226

All ages

There are a TON of resources on The Bridge,  so that’s a good place to start.

1) Blue Planet Series (recommended by @PaulSFenton on twitter) Great series, it’s on netflix and amazon

2) A Day in the life of a marine biologist (recommended by @Napaaqtuk  on twitter)

3) Diving Deep with Sylvia Earle (recommended by @Napaaqtuk  on twitter)

4) My wish: Protext our Oceans (Sylvia Earle) (also recommended by @Napaaqtuk  on twitter)

Adults

1) At the Water’s Edge (Recommended by @PaulSFenton on twitter) “More a book about evolution featuring marine animals but still a v. good read.“

2) Four Fish: The future of the last wild Food (Recommended by me!) A great book about fisheries

3) Kraken : The Curious, Exciting, and Slightly Disturbing Science of Squid (Recommended by me)

4) The Edge of the Sea by Rachel Carson (recommended by @MirandaRHK on twitter)

5) The Sea Around Us- Rachel Carson (Recommended by @aecahill on twitter)

6) An Unnatural History of the Sea- Callum Roberts

For you military history enthusiasts out there!

World War II in Southeast Asia as shown by this map, titled Japanese Centrifugal Offensive (offense?) and its clashes with other European forces occupying the region, December 1941 - April 1942.

In blue are notable major battles such as the Battles of Sunda Strait (February 28), Java Sea (February 27), Balikpapan (January 23 - 24), Lombok Straits (February 18 - 19). After the surprising Pearl Harbor attack the Japanese managed to curb the European defense over Southeast Asia, also in a surprising manner due to unpreparedness. 

[Larger view] - [more photos]

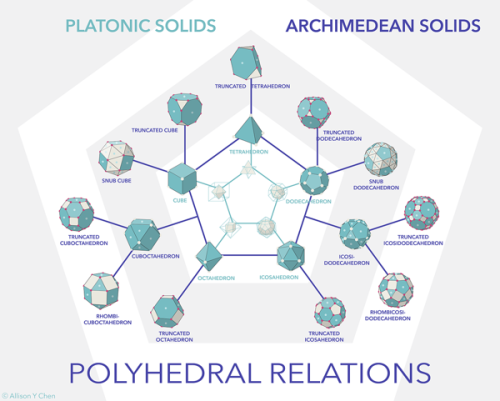
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

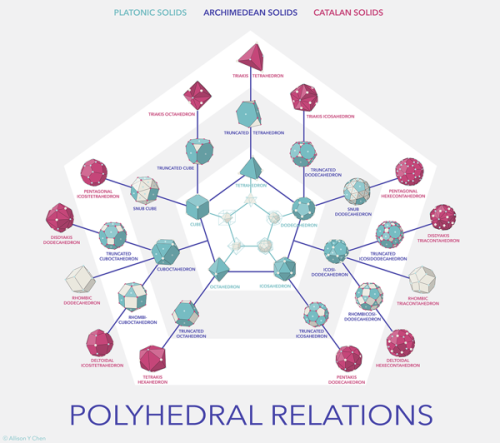
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

IT’S NATIONAL LIBRARY WEEK

HUZZAH! It is National Library Week, bookworms and library cats!! 

And that means it is the perfect time of year to show some love to your local (and not local) Libraries, both in person and online. So, just as we took time to make a special post on Follow a Library Day last year, we’ve created ANOTHER master post to honor all the libraries we know so far on tumblr so that you can #followalibrary!! 

Check out their tumblrs below and show them some love, bookworms! (Alphabetical by url)

@alachualibrary (The Alachua County Library District)

@alt-library (By Sacramento Public Library)

@aplibrary (Abilene Public Library)

@austinpubliclibrary (Austin Public Library)

@badgerslrc (The Klamath Community College’s Learning Research Center)

@bflteens (Baker Free Library’s Tumblr For Teens)

@bibliosanvalentino (Biblioteca San Valentino [San Valentino Library])

@biodivlibrary (Biodiversity Heritage Library)

@bodleianlibs (Bodleian Libraries)

@boonelibrary (Boone County Public Library)

@brkteenlib (Brookline Public Library Teen Services Department)

@californiastatelibrary (California State Library)

@cheshirelibrary (Cheshire Public Library)

@cityoflondonlibraries (City of London Libraries)

@cmclibraryteen (Cape May County Library’s Teen Services)

@cobblibrary (Cobb County Public Library System)

@cpl-archives (Cleveland Public Library Archives)

@cplsteens (Clearwater Public Library Teens)

@darienlibrary (Darien Library)

@dcpubliclibrary (DC Public Library)

@decaturpubliclibrary (Decatur Public Library)

@delawarelibrary (Delaware County District Library)

@detroitlib (Detroit Public Library Music, Arts & Literature Department)

@douglaslibraryteens (Douglas Library For Teens)

@dplteens (Danville Public Library Teens)

@escondidolibrary (Escondido Public Library)

@fontanalib (Fontana Regional Library)

@fppld-teens (Franklin Park Library Teens)

@friscolibrary (Frisco Public Library)

@gastonlibrary (Gaston County Public Library)

@glendaleteenlibrary (Glendale Public Library Teens)

@hpldreads (Havana Public Library District)

@hpl-teens (Homewood Public Library For Teens)

@kingsbridgelibraryteens (Kingsbridge Library Teens Advisory Group)

@lanelibteens (Lane Memorial Library Teen Services)

@lawrencepubliclibrary (Lawrence Public Library)

@marioncolibraries (Marion County Public Library System)

@mrcplteens (Mansfield/Richland County Public Library Teen Zone)

@myrichlandlibrary (Mansfield/Richland County Public Library)

@necclibrary (Northern Essex Community College Libraries)

@novipubliclibrary (Novi Public Library)

@nplteens (Nashua Public Library Teens)

@orangecountylibrarysystem (Orange County Library System)

@othmeralia  (Othmer Library of Chemical History)

@petit-branch-library (Petit Branch Library)

@pflibteens (Pflugerville Public Library Teenspace)

@plainfieldlibrary (Plainfield Public Library District)

@royhartlibrary (RoyHart Community Library)

@safetyharborpubliclibrary (Safety Harbor Library Teen Zone)

@santamonicalibr (Santa Monica Public Library)

@schlowlibrary (Schlow Centre Region Library)

@smithsonianlibraries (Museum Library System)

@smlibrary (Sheppard Memorial Library)

@southeastlibrary (Southeast Branch Library)

@tampabaylibraryconsortium-blog (Tampa Bay Library Consortium)

@teenbookerie (Erie County Public Library For Teens)

@teencenterspl (The Smith Public Library Teen Center)

@teensfvrl (Fraser Valley Regional Library)

@teen-stuff-at-the-library (White Oak Library District)

@therealpasadenapubliclibrary (Pasadena Public Library)

@ucflibrary (University of Central Florida Library)

@uwmspeccoll (University of Wisconsin Milwaukee Libraries Special Collections)

@vculibraries (Virginia Commonwealth University Libraries)

@waynecountyteenzone (Wayne County Public Library’s Teen Space)

@wellingtoncitylibraries (Wellington City Libraries)

@widenerlibrary (Harvard’s Widener Library)

Whew! There’s a LOT of you. :) But we now this list is just getting started! Feel free to keep the library love going by adding any libraries we missed/don’t know of yet! (And if you’re not following US already, well, what better time to start than this week? ;) Eh? Eh?) And, of course, never hesitate to visit your Library in person. We love seeing you! :) 

Happy National Library Week, library cats!

On March 3, 1923, Time published it’s first issue. In this prospectus, founders Henry Luce and Briton Hadden describe their vision for a news magazine “aimed to serve the modern necessity of keeping people informed, created on a new principle of COMPLETE ORGANIZATION.”

TIME The Weekly News-Magazine (A Prospectus). Time Inc. Records. New-York Historical Society.

1729

The number 1729 has an interesting story in mathematics involving the extraordinary Indian mathematician Srinivasa Ramanujan. G. H. Hardy accounts:

“I remember once going to see him (Ramanujan) when he was lying ill at Putney. I had ridden in taxi-cab No. 1729, and remarked that the number seemed to be rather a dull one, and that I hoped it was not an unfavourable omen. ‘No’, he replied, ‘it is a very interesting number; it is the smallest number expressible as the sum of two [positive] cubes in two different ways.’”

Ramanujan had a knack for numbers. Growing up in India at the turn of the 20th century, Ramanujan was largely self-taught. Over his short life time (aged 32), he independently developed nearly 4,000 results in mathematics. He kept his results (without proofs) in notebooks that modern mathematicians are still looking into this day. Nearly all of his results have been proven to be true and have driven research in number theory for the past century. Recently, one of Rumanujan’s results, previously unknown to mathematicians, was an important piece to a 2006 publication.

More at https://en.wikipedia.org/wiki/Srinivasa_Ramanujan

Oval Eggs

The word egg was a borrowing from Old Norse egg, replacing the native word ey (plural eyren) from Old English ǣġ, plural ǣġru.  Like “children” and “kine” (obsolete plural of cow), the plural ending -en was added redundantly to the plural form in Middle English.  As with most borrowings from Old Norse, this showed up first in northern dialects of English, and gradually moved southwards, so that for a while, ey and egg were used in different parts of England.

In 1490, when William Caxton printed the first English-language books, he wrote a prologue to his publication of Eneydos (Aeneid in contemporary English) in which he discussed the problems of choosing a dialect to publish in, due to the wide variety of English dialects that existed at the time.  This word was a specific example he gave.  He told a story about some merchants from London travelling down the Thames and stopping in a village in Kent 

And one of theym… cam in to an hows and axed for mete and specyally he axyd after eggys, and the goode wyf answerde that she could speke no Frenshe. And the marchaunt was angry, for he also coude speke no Frenshe, but wolde have hadde egges; and she understode hym not. And thenne at laste a-nother sayd that he wolde have eyren. Then the good wyf sayd that she understod hym wel. Loo, what sholde a man in thyse dayes now wryte, egges, or eyren? Certaynly it is hard to playse every man, by-cause of dyversite and chaunge of langage.

The merchant in this story was only familiar with the word egg, while the woman only knew ey, and the confusion was only resolved by someone who knew both words.  Indeed, the woman in the story was so confused by this unfamiliar word egg that she assumed it must be a French word!  The word “meat” (or “mete” as Caxton spelled it) was a generic word for “food” at the time.

The word ey may also survive in the term Cockney, thought to derive from the Middle English cocken ey (”cock’s egg”), a term given to a small misshapen egg, and applied by rural people to townspeople

Both egg and ey derived from the same Proto-Germanic root, *ajją, which apparently had a variant *ajjaz in West Germanic.  This Proto-Germanic form in turn derived from Proto-Indo-European *h2ōwyóm.  In Latin, this root became ōvum, from which the adjective ōvalis meaning “egg-shaped”, was derived.  Ōvum itself was borrowed into English in the biological sense of the larger gamete in animals, while ōvalis is the source of oval.

The PIE root is generally though to derive from the root *h2éwis, “bird”, which is the source of Latin avis “bird”, source of English terms such as aviation.  This word may also be related to *h2ówis “sheep”, which survived in English as ewe.  One theory is that they were both derived from a root meaning something like “to dress”, “to clothe”, with bird meaning “one who is clothed [in feathers]” and sheep meaning “one who clothes [by producing wool]”.

Word of the Day: potlatch

n. An opulent ceremonial feast (among certain North American Indian peoples of the north-west coast) at which possessions are given away or destroyed to display wealth or enhance prestige

Image: “Klallam people at Port Townsend” by James Gilchrist Swan. Public Domain via Wikimedia Commons

Types of mooncakes

Right now(is festival for chinese singaporeans) is the mid-autumn festival. According to the ancient Chinese legend, the story of Chang Er, the wife of a merciless king who downed the elixir of immortality he had intended to drink, to save her people from his tyrannical rule.The tale goes that she ascended to the moon after that, and has been worshipped by the Chinese as a Moon Goddess ever since. 

Making and sharing mooncakes is one of the hallmark traditions of this festival. In singapore, we have main five different chinese dialect group(hokkien,teochew,hakka,cantonese,hainanese) so of course, there are five different types of mooncakes.

CANTONESE MOOKCAKE

This is the most common style of mooncakes sold by bakeries and hotels. The round pastry, which is about 10cm in diameter and about 4cm thick, comes from south China’s Guangdong province and is also eaten in Hong Kong and Macau. The traditional mooncake is filled with lotus seed or red bean paste with egg yolks inside. 

However, there are the modern snowskin mooncakes which contains anything from durian to champagne. (below are champagne mooncakes)

HOKKIEN MOONCAKE

They were known as Scholar Cakes in the past and given to those taking the Imperial Examination to fill junior and senior administrative positions in the Imperial Court. The filling usually comprises winter melon, tangerine peel and melon seeds. Sesame seeds are sprinkled on the white pastry to make it fragrant.

HAINANESE MOONCAKE

Hainanese ones are filled with dried fruit such as tangerine peel as well as sesame seeds and melon seeds. It has two verision with a salty and pepper version. The.The slightly flaky skin is made with pork lard and salt. According to a blog, they are actually only found in singapore as the story goes that the hainanese community in singapore was very poor and could not afford the normal mooncakes sold so they made their own type of mooncake.

TEOCHEW MOONCAKE

Yam-filled mooncakes with a flaky crust are the most common Teochew mooncakes sold in Singapore. Another type is la gao, which is a steamed black sesame cake. It comes plain or with green bean paste or yam filling. There is also another type of Teochew mooncake, a white disc that looks like a big biscuit and is filled with tangerine peel and sugar, flavoured with five-spice powder and topped with sesame seeds.

HAKKA MOONCAKE

This is actually uncommon and almost unheard of in singapore but moon cakes in Hakka regions of china, apart from common moon cakes, have “five-kernel moon cakes” and a kind of round cake made with glutinous rice flour and sugar, compressed into different size. (I can’t find an exact picture of the hakka mooncake so)