Latest Posts by iphleandro-blog - Page 2

Here is a semester project in the 2012 Mechatronic control systems engineering module at San Jose State University. This is a Proportional-Integral-Derivative controlled (PID), 6 degree of freedom (6-DOF) Stewart platform, which basically means it has six axes on the top plate. This prototype uses 6 radio controlled servo motors instead of the traditional use of hydraulic jacks or electronic actuators. (this video has sound)

Proportional-Integral-Derivative:

A PID controller continuously calculates an error value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error over time by adjustment of a control variable, such as the position of a set of servo motors or actuators,  to a new value, given by a weighted sum:

where Kp ,Ki , and Kd, all non-negative, denote the coefficients for the proportional, integral, and derivative terms, respectively (sometimes denoted P, I, and D).

P accounts for present values of the error , and is determined by the direction and magnitude the correction needs to be applied (e.g. if the error is large and positive, the control variable will be large and negative),

I accounts for past values of the error (e.g. if the output is not sufficient to reduce the size of the error, the control variable will accumulate over time, causing the controller to apply a stronger action through P), and

D accounts for possible future values of the error, based on its current rate of change. This part determines when and at what rate it needs to reduce the magnitude of its action, e.g as the ball fast approaches the desired set point at the centre of the plate.

[source]

Leap Day…Why Does It Exist?

Once every four years, an extra calendar day is added: a leap day. But why?

The reason for adding leap days to the calendar is to align the calendar year with the actual year – which is defined by the time it takes Earth to circle the sun. It is equal to 365 days, 5 hours, 48 minutes and 46 seconds, or 365.24219 days.

If all calendar years contained exactly 365 days, they would drift from the actual year by about 1 day every 4 years. Eventually, July would occur during the northern hemisphere winter! Wouldn’t that be weird?

To correct (approximately), we add 1 day every 4 years…resulting in a leap year.

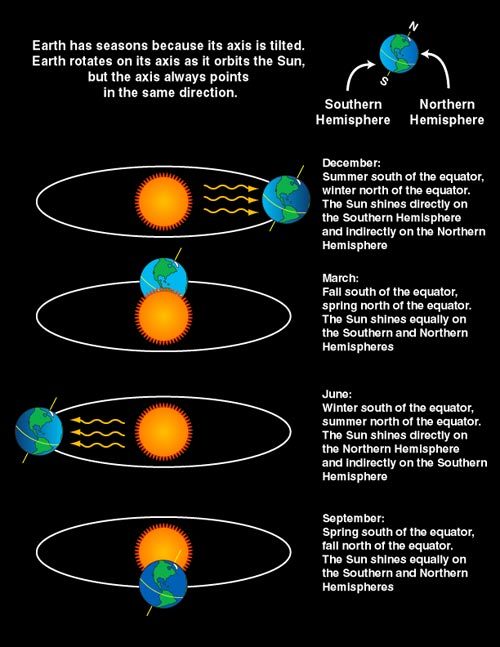
By making most years 365 days but every fourth year 366 days, the calendar year and the actual year remain more nearly in step.

Make sure to follow us on Tumblr for your regular dose of space: http://nasa.tumblr.com

That’s how a revolving fan works

This gif has been circulating throughout the internet for many years, and I am not denying it It’s pretty darn cool!

Although it gets the mechanism spot on, but it misses out on one of the most amazing part of the mechanism : the oscillation itself.

How does it oscillate?

                       Source

The oscillation is simple but ingenious. So, you see that pink rod? Yeah that is attached to v - type wedge, like so:

89 is a pin. And that pin is constrained to oscillate between the two wedges. The angle of oscillation is primarily between 40-100 degrees.

It is this wedge that controls the oscillation.

Why does it oscillate?

The oscillation is due to an eccentric round cam present under the yellow gear. ( seen in animation too )

An eccentric cam

The rotation of this cam induces a torque which causes the linkage ( the pink rod ) to sweep across the plane.

Important Note

I understand that this explanation is not exactly the finest. But this mechanism has not been explored anywhere else on the Internet .This is what i could reckon of the Patent.

If you have a better explanation/sources/anything at all then please reblog it with this post, that way everyone wins. It is our humble request.

Have a good day!

Can you flatten a sphere?

The answer is NO, you can not. This is why all map projections are innacurate and distorted, requiring some form of compromise between how accurate the angles, distances and areas in a globe are represented.

This is all due to Gauss’s Theorema Egregium, which dictates that you can only bend surfaces without distortion/stretching if you don’t change their Gaussian curvature.

The Gaussian curvature is an intrinsic and important property of a surface. Planes, cylinders and cones all have zero Gaussian curvature, and this is why you can make a tube or a party hat out of a flat piece of paper. A sphere has a positive Gaussian curvature, and a saddle shape has a negative one, so you cannot make those starting out with something flat.

If you like pizza then you are probably intimately familiar with this theorem. That universal trick of bending a pizza slice so it stiffens up is a direct result of the theorem, as the bend forces the other direction to stay flat as to maintain zero Gaussian curvature on the slice. Here’s a Numberphile video explaining it in more detail.

However, there are several ways to approximate a sphere as a collection of shapes you can flatten. For instance, you can project the surface of the sphere onto an icosahedron, a solid with 20 equal triangular faces, giving you what it is called the Dymaxion projection.

The Dymaxion map projection.

The problem with this technique is that you still have a sphere approximated by flat shapes, and not curved ones.

One of the earliest proofs of the surface area of the sphere (4πr2) came from the great Greek mathematician Archimedes. He realized that he could approximate the surface of the sphere arbitrarily close by stacks of truncated cones. The animation below shows this construction.

The great thing about cones is that not only they are curved surfaces, they also have zero curvature! This means we can flatten each of those conical strips onto a flat sheet of paper, which will then be a good approximation of a sphere.

So what does this flattened sphere approximated by conical strips look like? Check the image below.

But this is not the only way to distribute the strips. We could also align them by a corner, like this:

All of this is not exactly new, of course, but I never saw anyone assembling one of these. I wanted to try it out with paper, and that photo above is the result.

It’s really hard to put together and it doesn’t hold itself up too well, but it’s a nice little reminder that math works after all!

Here’s the PDF to print it out, if you want to try it yourself. Send me a picture if you do!

Calculating the surface area of a sphere. Found on Imgur.

A beautiful geometric visualization of positive-valued binomial expansions, the algebraic expressions produced by raising sums of variables (a, b) to natural-valued powers n. The algebraic structures and procedures of binomial expansion are described by the binomial theorem–which, in turn, is proved by the above figures. 

Given (a+b)^n, there will be (n+1)-many terms, c(a^(n-m))(b^m), where c is a constant, and a and b are variables. 

By tradition, these terms are arranged in descending order by powers of the leading term, a. Accordingly, the binomial expansion of (a+b)^n begins with the term having the highest power of a, which is a^n for all n. 

The remaining n-many terms are ordered such that the exponent of each successive a term (n-m) decreases by one. Correspondingly, the exponent of the b term (m) increases by one, such that (n-m)+m=n. 

The binomial coefficients c for each successive term c(a^(n-m))(b^m) are described by Pascal’s triangle. Given (a+b)^n, the nth row of Pascal’s triangle contains (n+1)-many numbers, which are the coefficients c, listed in the order described above.

Note that the exponent n is the dimension of the figures pictured above. This is no coincidence; the term (a+b)^n can be depicted geometrically by a figure whose measure (length, area, volume, hypervolume, etc.) is the quantity produced by multiplying (a+b), n-many times. 

Additionally, observe that the coefficients c give the quantity of n-dimensional figures required to fill in the missing bits of area, as illustrated by the figures. For example, in order to fill the volume (a+b)^3, we use two cubes of volume a^3 and b^3, and the remainder is filled by 3 “plate-like” figures and 3 “tube-like” figures (each of whose dimensions are (a^2)b and a(b^2), respectively).

Mathematics is beautiful. <3

Alberto Camara  -  http://camarasketch.tumblr.com  -  https://society6.com/albertocamara/prints  -  https://www.instagram.com/camarasketch  -  https://camarasketch.deviantart.com  -  https://twitter.com/Camarasketch

Majestic Volcano

Glacial Striations and Stromatolites and Geology, oh my!

This photo is a two-fer: two awesome geology features in one! On the surface of this rock you will notice faint lines that stretch from the lower left hand corner of the image to the upper right hand corner. These lines are called glacial striations and they form as a glacier scratches the rock surface as it moves. 

The rock surface that was scratched by the moving glacier represents an entirely different time, waaay before the glaciers, when stromatolites dotted the shoreline of an ancient water body that covered Montana. The circles that you see in the rock are the tops of stromatolites, formed by ancient cyanobacteria. 

A great place to see stromatolites and striations is on the Grinnell Glacier Trail. For your best chance of seeing these features free of snow, try hiking the trail in late July or August. NPS Photo

[Image Description: Lines and circles etched into a rock surface.]

fms.fossils

Here was a lucky little find from today’s fossil hunt on Charmouth beach. This is a pyrite ammonite of the species Echioceras raricostatum. They are preserved in very soft shale, as you can see, which means that they come out in one piece very easily. Usually, the sea pulls them out of the rocks and dumps them on the beach. This can easily damage or destroy them. This one has a thin calcite shell on top of the pyrite which would have been removed by the sea almost instantly if it had got to it before I did. This fossil is around 196 million years old.

Survival Tips For Your Life

INKTOBER DAY 13 to 21!!!  #21 DRAIN #20 BREAKABLE #19 SCORCHED #18 BOTTLE #17 SWOLLEN #16 ANGULAR #15 WEAK #14 CLOCK #13 GUARDED

“Baignade en rivière” again

This enormous wolf

OH MY GOD

Kids parenting.  

Give your child a warm embrace.

Erta Ale volcano lava lake, Ethiopia

alfonso.pop

galihadventure

Typical Vulcanian Eruption! A lot of lava boms thrown up from the crater!

Batalla épica con final inesperado

Map of US National Parks

Camping tip

Horseshoe Bend, AZ. Watched the sunset and it was everything I could have hoped for on a roadtrip. [6000x4000][OC] https://ift.tt/2Ppvm1A

Hey Tumblr! I found an awesome travel contest that I want to share with my followers. Travel for free to France, The Netherlands, Switzerland, or Serbia. Just click here and read my blog for more details!

The Bortle Scale and Light Pollution

The Bortle Scale is used by astronomers to rate the darkness of our skies. It ranges from 1 (darkest) to 9 (brightest). For most of us, our daily lives are spent beneath a radiance level of between 5 and 8 and rarely venture into areas ranked 3 or darker- and what a shame that is.

Light pollution, while a testament to our technological advances, has blanketed our view of the universe and decoupled our relationship with the cosmos. For the millions of people living in areas where less than 20 stars can be seen in the night sky, it is practically impossible to imagine a natural sky blanketed with upwards of 2,500 stars backed by great ribbons of billions of stars which can be found in our Galaxy: The Milky Way.

What are the effects of light pollution?

Continuar lendo

x

hannah__dawn 🐉

douggsbase This was the 4th big way I have organised at Kjerag, Norway and the local record of 26 jumpers. The last record held here was a 24 way back in 1999. It went incredibly well. Text book in fact! And for most people this was their first big way. 20 jumpers were from @learntobasejump#LTBJA huge thanks to everyone for doing their jobs. I am very proud of all of you!! Big thanks to @sophiimeredithfor the great video angle 🎥

Cute animals ♥