Ah Yes My Boy Tom Cardy. Everyone Must Listen To Him, He's The Best

today I learned that for a surface with boundary, which I believe we can say a straw is, the genus is equal to that of a 2-manifold obtained from attaching disks to the boundary. hence the straw has genus equal to that of a 2-sphere, which is 0, therefore a straw has 0 holes

also a straw is not homotopic to a torus I think, but rather to S¹, as it's a product of S¹ and a closed interval, which is contractible. a torus has the fundamental group S¹×S¹, thus they cannot be homotopy equivalent. buuut that requires the straw to be infinitely thin so maybe I'm too idealistic for this claim to hold and it is in fact equivalent to a torus

lmao I love math but I can't stop laughing at the fact that it took me two years of university to be able to have this discussion

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

→ 3 IX 2021

such a weird day today. i finished complete spaces and then moved on to preparing for the math conference i'm going to on sunday. there is a lot of high level stuff so i won't be able to learn everything, of course, but i'm doing my fav thing ever and enjoying it thoroughly. that is, switching from a topic to a topic in the spare of 15 minutes and reading a bit about anything until it stops being ✨super exciting✨

this amounts to a total of 8 hours of math and i am not done yet. love it, absolutely love to waste time like that

concentration: fucking ∞

tomorrow i'm doing an algebra speedrun with bf and two of our friends. this is an experiment aiming at seeing how much information we are able to pack into our heads in one sitting. we haven't studied abstract algebra before. then in a few as i mentioned i am going to a math conference, with bf and our other friend. excited about that too. i fucking love math

Zero to the power of anything is zero. Anything to the zeroth power is one. So what is zero to the zeroth power?

The world's most cited mathematicians would seem to be in disagreement about the issue

oh, you misunderstood. when i said "applications" i didnt mean real world applications, i meant ways to use this in the context even more abstract nonsense

13 III 2023

I remember putting it in my bio a while ago that I dream of doing actual research one day. well this is already happening, as I mentioned in some post, my advisor found an open question for me to write my thesis about

the progress for now is that I'm done with most of the reading I need to do to tackle it and I'm slowly moving forward with thinking of ideas for the solution (or at least a partial one)

this is what I want to do for the rest of my life: reading papers and trying to write my own ones

ofc I don't know if I manage to solve the problem or achieve anything at all with it but the process itself is fun

other than that I've been catching up with homeworks and assignments from work. fortunately I found an MIT lecture recordings for statistics so hopefully I might not die from boredom

watching probability and stats lectures from MIT has been my relationship's idea of netflix and chill for a while now, gotta cultivate the tradition

the algtop professor asked us to write down a full detailed solution for an exercises we did in class, because the person presenting was unable to explain it so I sent him mine

I don't know yet if it's correct but I'm pretty sure it is. I wrote this down partly because who doesn't want extra points and partly because I didn't have a chance to present it, the person who did was faster

I like how my life is right now, I want to keep it that way

My favourite fucked up math fact™ is the Sharkovskii theorem:

For any continuous function f: [a,b] -> [a,b], if there exists a periodic point of order 3 (i.e. f(f(f(x))) = x for some x in [a,b] and not f(x) = x or f²(x) = x), then there exists a periodic point of ANY order n.¹

Yes you read that right. If you can find a point of order 3 then you can be sure that there is a point of order 4, 5, or even 142857 in your interval. The assumption is so innocent but I cannot understate how ridiculous the result is.²

For a (relatively) self-contained proof, see this document (this downloads a pdf).

(footnotes under read more)

¹ The interval does not have to be closed, but it should be connected. (a,b), (a,b] and [a,b) all work.

² Technically the result is even stronger! The natural numbers admit a certain ordering called the Sharkovskii ordering which starts with the odd primes 3 > 5 > 7 > ... , then doubles of primes, then quadruples of primes and so forth until you get no more primes left, ending the ordering in 2³ > 2² > 2. Sharkovskii's theorem actually says that if you have a periodic point of order k, then you have periodic points of any order less than k in the Sharkovskii ordering. It is frankly ridiculous how somehow prime numbers make their way into this mess.

some more animation: how secant-teenager becomes tangent-adult

also! it illustrates a well-known inequality of a differentiable convex function and its tangents & the monotony of slopes

hey be nice to me im just a teenage girl who has legally been an adult for years

Thank you, /r/ProgrammerHumor, I love you endlessly.

Redditors competing to make the worst volume sliders possible...

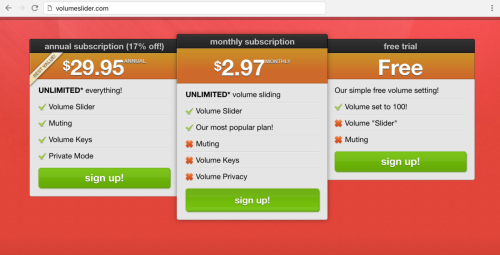
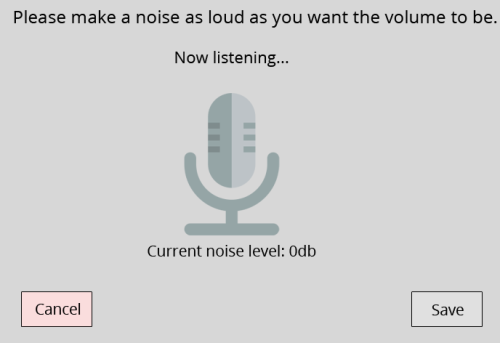
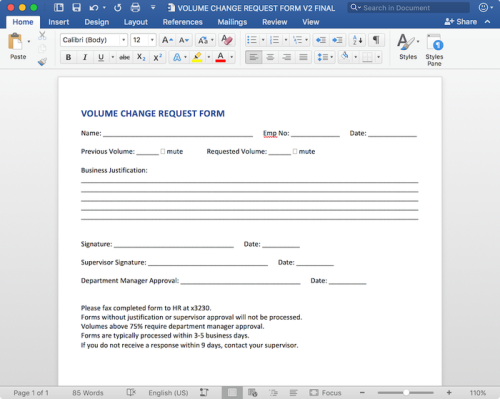
If you want to rizz up a mathematician, just tell them that they "proved love at first sight exists by giving an explicite example".